A CSP (Constraints Satisfaction Problem) is defined on a finite set of variables:

• (X1, X*2 ..., Xn) decisions that we have to take

• (D1, D2 ..., Dn) domains of possible values

• a set of constraints.

• No propagation algorithms:

  • Generate and Test， GT
  • Backtracking Standard，BS

• Propagation Algorithms

  • Forward Checking，FC
  • (Partial and Full) Look Ahead， PLA/FLA

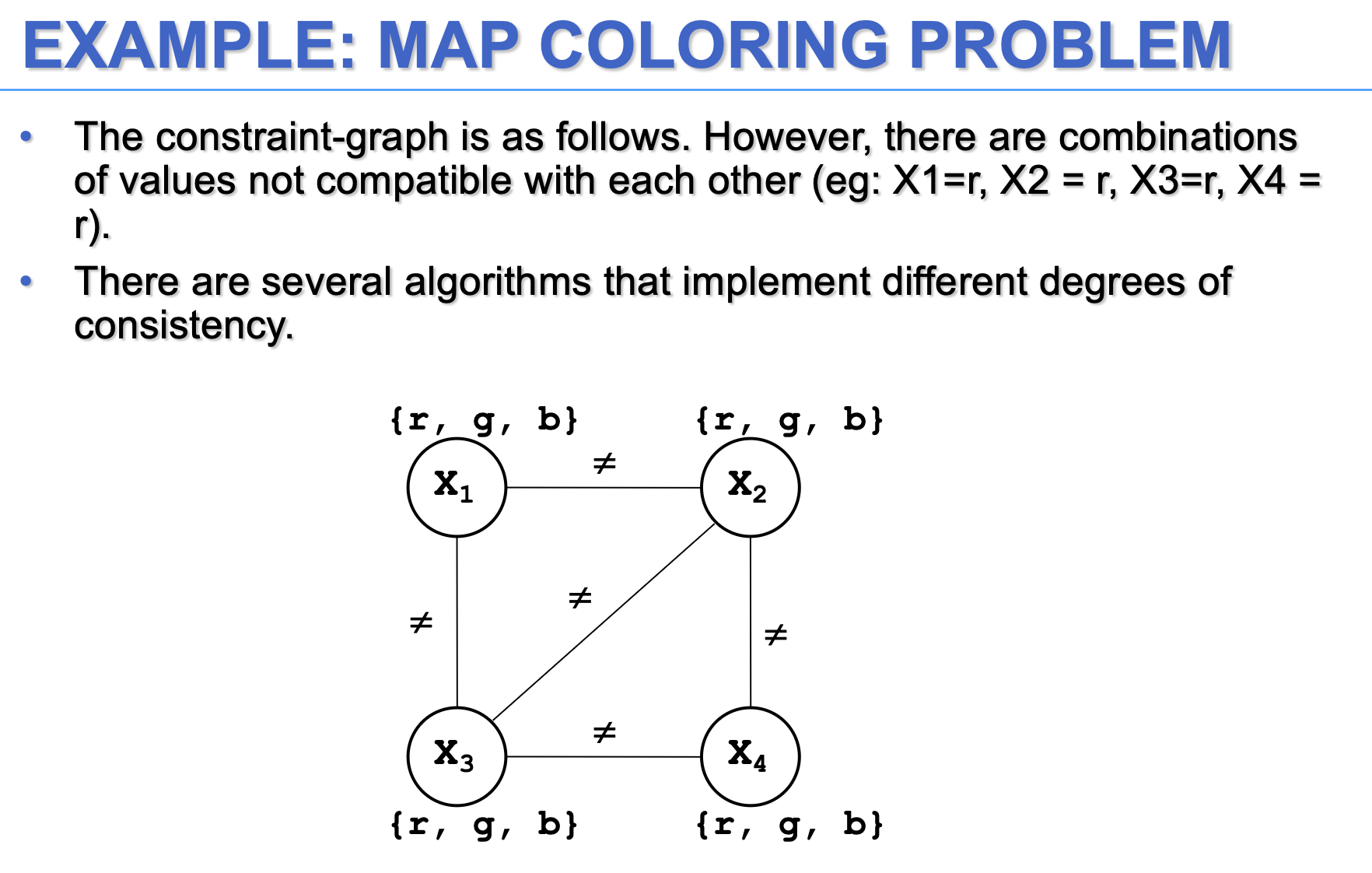
CONSTRAINT GRAPH

For each CSP exists a graph (constraint graph) in which the nodes represent variables and the arcs are the constraints.

• The binary constraints (R) connecting two nodes Xi and Xj:
• The unary constraints are represented by arcs that begin and end on the same node Xi
• ![[截屏2026-01-16 17.11.25.png]
• 
• Node consistency
• Arc consistency
• Path consistency

Exercise

• 
• 
• 每当为一个变量 Xi​ 分配一个值时，FC 会检查所有包含 Xi​ 且涉及尚未实例化变量的约束，如果对于已分配的Xi，其他有关变量有不兼容的数值，则将不兼容的数值从对应的domain删掉。
• 对于PLA，为Xi赋值后，先做FC的检查，再依照字母顺序检查下一个未赋值变量（$X_{i+1}$）的domain中是否有不符合($X_{i+1}$与之后的变量的)约束其它的值，有不符合的就删掉。
• 对于FLA，先做PLA，检查所有其它变量与Xi是否有不兼容的值。